链表
链表逆置
js
function reverse(head) {
let pre = null, next = null;
while (head !== null) {
next = head.next;
head.next = pre;
pre = head;
head = next;
}
return pre;
}链表指定区间内反转
TIP
思路：创建一个虚拟头结点，方便反转操作。
js
function reverseBetween(head, m, n) {
let dummpy = new ListNode(-1);
dummpy.next = head;
let pre = dummpy, cur = head, next = null;
for (let i = 0; i < m - 1; i++) {
pre = pre.next;
cur = cur.next;
}
for (let i = 0; i < n - m; i++) {
next = cur.next;
cur.next = cur.next.next;
next.next = pre.next;
pre.next = next;
}
return dummpy.next;
}合并两个排序的链表
js
function Merge( pHead1 , pHead2 ) {
// 确定 p1 为最终答案
if (!pHead1) {
return pHead2;
}
if (!pHead2) {
return pHead1;
}
let h1 = pHead1, h2 = pHead2;
if (h1.val > h2.val) {
pHead1 = h2;
pHead2 = h1;
}
let dummpy = new ListNode(-1);
dummpy.next = pHead1;
let p1 = pHead1, p2 = pHead2, pre = dummpy;
while (p1 && p2) {
if (p1.val > p2.val) {
let next = p2.next;
pre.next = p2;
p2.next = p1;
p2 = next;
} else {
p1 = p1.next;
}
pre = pre.next;
}
if (p1) {
pre.next = p1;
}
if (p2) {
pre.next = p2;
}
return dummpy.next;
}合并k个已排序的链表
TIP
思路：使用优先队列（小根堆），将 k 个链表的头节点先按照从小到大的顺序放入优先队列。
java
public class Solution {
public ListNode mergeKLists (ArrayList<ListNode> lists) {
PriorityQueue<ListNode> heap = new Priority<>((a, b) -> a.val - b.val);
for (ListNode head : lists) {
heap.add(head);
}
if (heap.isEmpty()) {
return null;
}
// 取出第一个当作总的头结点
ListNode head = heap.poll(), p = head;
if (head.next) {
heap.add(head.next);
}
while (!heap.isEmpty()) {
ListNode cur = heap.poll();
p.next = cur;
p = cur;
if (cur.next) {
heap.add(cur.next);
}
}
}
}判断链表是否有环
TIP
思路：快慢指针。快指针一次走两步，慢指针一次走一步。如果两者能相遇，则表明链表必定有环。
js
function hasCycle(head) {
if (!head || !head.next || !head.next.next) return false;
let slow = head, fast = head.next.next;
while (fast && fast.next && slow !== fast) {
slow = slow.next;
fast = fast.next.next;
}
if (!fast || !fast.next) {
return false;
}
if (slow === fast) {
return true;
}
}链表中环的入口节点
TIP
思路：快慢指针。快指针一次走两步，慢指针一次走一步。当两者相遇时，让快指针回到开头，快、慢指针每次各走一步，直到两者相遇，相遇的那个节点就是环的入口节点。
js
function entryNodeOfLoop(pHead) {
if (!pHead || !pHead.next || !pHead.next.next) return null;
let slow = pHead, fast = pHead.next.next;
while (fast && fast.next && slow !== fast) {
slow = slow.next;
fast = fast.next.next;
}
if (!fast || !fast.next) return null;
fast = pHead;
while (fast !== slow) {
fast = fast.next;
slow = slow.next;
}
return slow;
}链表中倒数最后k个节点
TIP
思路：快慢指针。先找长度再找最后 k。 先让快指针走 k 步，再让慢指针从头开始，两个指针往后移，直到快指针走到头，此时慢指针指向的节点就是倒数最后 k 个节点。
js
function findKthToTail(pHead, k) {
if (k < 0) return null;
let fast = pHead, slow = pHead;
let length = 0;
while (fast) {
length++;
fast = fast.next;
}
if (k > length) return null;
fast = pHead;
while (k-- > 0 && fast) {
fast = fast.next;
}
while (fast) {
fast = fast.next;
slow = slow.next;
}
return slow;
}两个链表的第一个公共节点
TIP
思路：先求出两个链表长度差 diff，让长的那个链表线移动 diff 步。然后，两个链表同时移动，直到相遇，相遇的那个节点就是第一个公共节点。
js
function FindFirstCommonNode(pHead1, pHead2) {
if (pHead1 === null || pHead2 === null) {
return null;
}
// 分别获取 pHead1 和 pHead2 的链表长度
let len1 = 0, len2 = 0;
let h1 = pHead1, h2 = pHead2;
while(h1 !== null) {
len1++;
h1 = h1.next;
}
while(h2 !== null) {
len2++;
h2 = h2.next;
}
h1 = len1 > len2 ? pHead1 : pHead2;
h2 = len1 <= len2 ? pHead1 : pHead2;
// 先让 h1 走 |len1 - len2| 个节点
let diff = Math.abs(len1 - len2);
while (diff-- > 0) {
h1 = h1.next;
}
// 然后 h1 和 h2 一块走，直到相遇
while (h1 !== h2) {
h1 = h1.next;
h2 = h2.next;
}
return h1;
}链表相加
TIP
思路：先将两个链表逆置，然后再进行链表相加即可。
js
function addInList( head1 , head2 ) {
// write code here
if (head1.val === 0 || head2.val === 0) {
return head1.val === 0 ? head2 : head1;
}
return reverse(add(reverse(head1), reverse(head2)));
}
const reverse = (head) => {
let last = null;
let cur = head;
while (cur) {
let tmp = cur.next;
cur.next = last;
last = cur;
cur = tmp;
}
return last;
}
const add = (h1, h2) => {
// 进制数
let carry = 0;
let ans = null, cur = null;
for (let sum = 0, value = 0;
h1 !== null || h2 !== null;
h1 = h1 === null ? null : h1.next,
h2 = h2 === null ? null : h2.next) {
sum = (h1 === null ? 0 : h1.val) +
(h2 === null ? 0 : h2.val) +
carry;
value = sum % 10;
carry = Math.floor(sum / 10);
if (!ans) {
ans = new ListNode(value);
cur = ans;
} else {
cur.next = new ListNode(value);
cur = cur.next;
}
}
if (carry !== 0) {
cur.next = new ListNode(carry);
}
return ans;
}双指针
盛最多水的容器
TIP
思路：通过对向指针来解答本题。
js
function maxArea(height) {
let ans = 0;
for (let l = 0, r = height.length - 1; l < r; ) {
ans = Math.max(ans, Math.min(height[l], height[r]) * (r - l));
if (height[l] <= height[r]) {
l++;
} else {
r--;
}
}
return ans;
}三数之和
TIP
从头到尾遍历，内部使用对向指针。
js
function threeSum(nums) {
let ans = [];
for (let i = 0; i < nums.length; i++) {
if (nums[i] > 0) return ans;
if (i > 0 && ums[i] === nums[i - 1]) continue;
let l = i + 1, r = nums.length - 1;
while (l < r) {
let sum = nums[i] + nums[l] + nums[r];
if (sum === 0) {
ans.push([nums[i], nums[l], nums[r]]);
while (r > l && nums[r] === nums[r - 1]) r--;
while (r > l && nums[l] === nums[l - 1]) l++;
r--;
l++;
} else if (sum < 0) {
l++;
} else {
r--;
}
}
}
return ans;
}接雨水
TIP
接雨水我们其实要求的就是每个位置上面能存多少雨水，然后把每个位置上的雨水相加即可。
每个位置上面能存的雨水 = max{0, min{左边的最大值，右边的最大值} - 当前位置的值}
- 分别维护一个左边最大值和右边最大值的数组
- 直接使用双指针
方法1：
js
function trap(height) {
let n = height.length;
let lmax = Array.from(n, () => 0), rmax = Array.from(n, () => 0);
lmax[0] = height[0];
for (let i = 1; i < n; i++) {
lmax[i] = Math.max(lmax[i - 1], height[i]);
}
rmax[n - 1] = height[n - 1];
for (let i = n - 2; i >= 0; i--) {
rmax[i] = Math.max(rmax[i + 1], height[i]);
}
let ans = 0;
for (let i = 1; i < n - 1; i++) {
ans += Math.max(0, Math.min(lmax[i - 1], rmax[i + 1]) - height[i]);
}
return ans;
}方法2：
js
function trap(height) {
let n = height.length, lmax = height[0], rmax = height[n - 1], l = 1, r = n - 2;
let ans = 0;
while (l <= r) {
if (lmax <= rmax) {
ans += Math.max(0, lmax - height[l]);
lmax = Math.max(lmax, height[l++]);
} else {
ans += Math.max(0, rmax - height[r]);
rmax = Math.max(rmax, height[r--]);
}
}
return ans;
}归并排序
IMPORTANT
主要利用分治思想，时间复杂度 O(nlogn)。
- 对数组不断等长拆分，直到一个数的长度。
- 回溯时，按升序合并左右两段。
- 重复以上两个过程，直到递归结束。
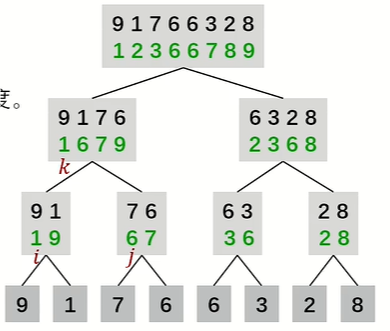
归并排序模板
js
// 辅助数组
let help = [];
function merge(l, r) {
if (l === r) return;
let mid = Math.floor((l + r) / 2);
merge(l, mid);
merge(mid + 1, r);
let i = l, j = mid + 1, k = l;
while (l <= mid && j <= r) {
if (nums[i] <= nums[j]) {
help[k++] = nums[i];
} else {
help[k++] = nums[j];
}
}
while (i <= mid) help[k++] = nums[i++];
while (j <= r) help[k++] = nums[j++];
for (i = l, i <= r; i++) nums[i] = help[i];
}逆序对
js
const MOD = 1000000007;
function InversePairs(nums) {
let help = [], ans = 0;
function merge(l, r) {
if (l === r) return;
let mid = Math.floor((l + r) / 2);
merge(l, mid);
merge(mid + 1, r);
let i = l, j = mid + 1, k = l;
while (i <= mid && j <= r) {
if (nums[i] <= nums[j]) {
help[k++] = nums[i++];
} else {
help[k++] = nums[j++];
ans += (mid - i + 1) % MOD;
}
}
while (i <= mid) help[k++] = nums[i++];
while (j <= mid) help[k++] = nums[j++];
for (i = l; i <= r; i++) {
nums[i] = help[i];
}
}
merge(0, nums.length - 1);
return ans % MOD;
}bfs 及其拓展
bfs 模板
IMPORTANT
bfs 的特点是逐层扩散，从源头点到目标点扩散了几层，最短路就是多少
bfs 可以使用的特征是 任意两个节点之间的相互距离相同（无向图）
bfs 开始时，可以是 单个源头、也可以是 多个源头
bfs 频繁使用队列，形式可以是 单点弹出 或者 整层弹出
bfs 进行时，进入队列的节点需要标记状态，防止 同一个节点重复进出队列
bfs 进行时，可能会包含 剪枝策略 的设计
js
const MAXN = 101;
const MAXM = 101;
let queue = Array.from({length: MAXM * MAXN}, () => Array.from({length: 2}, () => 0));
let l, r;
let visited = Array.from({length: MAXN}, () => Array.from({length: MAXM}, () => false));
let move = [-1, 0, 1, 0, -1];
const maxDistance = (grid) => {
l = r = 0;
let n = grid.length;
let m = grid[0].length;
let seas = 0;
for (let i = 0; i < n; i++) {
for (let j = 0; j < m; j++) {
if (grid[i][j] === 1) {
visited[i][j] = true;
queue[r][0] = i;
queue[r++][1] = j;
} else {
visited[i][j] = false;
seas++;
}
}
}
if (seas === 0 || seas === n * m) {
return -1;
}
let level = 0;
while (l < r) {
level++;
let size = r - l;
for (let k = 0, x, y, nx, ny; k < size; k++) {
x = queue[l][0];
y = queue[l++][1];
for (let i = 0; i < 4; i++) {
nx = x + move[i];
ny = y + move[i + 1];
if (nx >= 0 && nx < n && ny >= 0 && ny < m && !visited[nx][ny]) {
visited[nx][ny] = true;
queue[r][0] = nx;
queue[r++][1] = ny;
}
}
}
}
return level - 1;
};01bfs 模板
IMPORTANT
01bfs 思想：
01bfs，适用于图中所有边的权重只有 0 和 1 两种值，求源点到目标点的最短距离 时间复杂度为 O(节点数量+边的数量)
distance[i]表示从源点到i点的最短距离，初始时所有点的distance设置为无穷大源点进入
双端队列，distance[源点]=0双端队列
头部弹出 x，A. 如果
x是目标点，返回distance[x]表示源点到目标点的最短距离B. 考察从
x出发的每一条边，假设某边去y点，边权为w 1）如果
distance[y] > distance[x] + w，处理该边；否则忽略该边 2）处理时，更新
distance[y] = distance[x] + w 如果
w==0，y从头部进入双端队列； 如果
w==1，y从尾部进入双端队列。 3）考察完
x出发的所有边之后，重复步骤3双端队列为空停止
js
const minimumObstacles = (grid) => {
let move = [-1, 0, 1, 0, -1];
let m = grid.length;
let n = grid[0].length;
let distance = Array.from({length: m}, () => Array.from({length: n}, () => Number.MAX_VALUE));
let deque = [];
let l = 0, r = 0;
deque.push([0, 0]);
distance[0][0] = 0;
while (deque.length !== 0) {
let record = deque.shift();
let x = record[0];
let y = record[1];
if (x === m - 1 && y === n - 1) {
return distance[x][y];
}
for (let i = 0; i < 4; i++) {
let nx = x + move[i], ny = y + move[i + 1];
if (nx >= 0 && nx < m && ny >= 0 && ny < n && distance[x][y] + grid[nx][ny] < distance[nx][ny]) {
distance[nx][ny] = distance[x][y] + grid[nx][ny];
if (grid[nx][ny] === 0) {
deque.unshift([nx, ny]);
} else {
deque.push([nx, ny]);
}
}
}
}
return -1;
}js
const minCost = (grid) => {
let move = [[], [0, 1], [0, -1], [1, 0], [-1, 0]];
let n = grid.length;
let m = grid[0].length;
let distance = Array.from({length: n}, () => Array.from({length: m}, () => Number.MAX_VALUE));
let deque = [];
deque.push([0, 0]);
distance[0][0] = 0;
while (deque.length !== 0) {
let record = deque.shift();
let x = record[0];
let y = record[1];
if (x === n - 1 && y === m - 1) {
return distance[x][y];
}
for (let i = 1; i <= 4; i++) {
let nx = x + move[i][0];
let ny = y + move[i][1];
let weight = grid[x][y] !== i ? 1 : 0;
if (nx >= 0 && nx < n && ny >= 0 && ny < m && distance[x][y] + weight < distance[nx][ny]) {
distance[nx][ny] = distance[x][y] + weight;
if (weight === 0) {
deque.unshift([nx, ny]);
} else {
deque.push([nx, ny]);
}
}
}
}
return -1;
};Dijkstra算法
IMPORTANT
普通堆实现的 Dijkstra 算法，时间复杂度 O(m * log m)，m 为边数
distance[i]表示从源点到i点的最短距离，visited[i]表示i节点是否从小根堆弹出过准备好小根堆，小根堆存放记录：(
x点，源点到x的距离)，小根堆根据距离组织令
distance[源点]=0，(源点，0)进入小根堆从小根堆弹出(
u点，源点到u的距离) a. 如果visited[u] == true，不做任何处理，重复步骤4b. 如果
visited[u] == false，令visited[u] = true，u就算弹出过了 然后考察
u的每一条边，假设某边去往v，边权为w 1）如果visited[v] == false并且distance[u] + w < distance[v] 令distance[v] = distance[u] + w，把(v, distance[u] + w)加入小根堆 2）处理完u的每一条边之后，重复步骤45，小根堆为空过程结束，distance表记录了源点到每个节点的最短距离。
普通堆实现 Dijkstra 算法模板
java
class Solution {
public int networkDelayTime(int[][] times, int n, int k) {
ArrayList<ArrayList<int[]>> graph = new ArrayList<>();
for (int i = 0; i <= n; i++) {
graph.add(new ArrayList<>());
}
for (int[] edge : times) {
graph.get(edge[0]).add(new int[]{edge[1], edge[2]});
}
int[] distance = new int[n + 1];
distance[k] = 0;
boolean[] visited = new boolean[n + 1];
PriorityQueue<int[]> heap = new PriorityQueue<>((a, b) -> a[1] - b[1]);
heap.add(new int[]{k, 0});
while (!heap.isEmpty()) {
int u = heap.poll()[0];
if (visited[u]) {
continue;
}
visited[u] = true;
for (int[] edge : graph.get(u)) {
int v = edge[0];
int w = edge[1];
if (distance[u] + w < distance[v]) {
distance[v] = distance[u] + w;
heap.add(new int[]{v, distance[u] + w});
}
}
}
int ans = Integer.MIN_VALUE;
for (int i = 1; i <= n; i++) {
if (distance[i] == Integer.MAX_VALUE) {
return -1;
}
ans = Math.max(ans, distance[i]);
}
return ans;
}
}java
class Solution {
public static int[] move = new int[]{-1, 0, 1, 0, -1};
public int minimumEffortPath(int[][] heights) {
ArrayList<ArrayList<int[]>> graph = new ArrayList<>();
int n = heights.length;
int m = heights[0].length;
int[][] distance = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
distance[i][j] = Integer.MAX_VALUE;
}
}
distance[0][0] = 0;
boolean[][] visited = new boolean[n][m];
PriorityQueue<int[]> heap = new PriorityQueue<>((a, b) -> a[2] - b[2]);
heap.add(new int[]{0, 0, 0});
while (!heap.isEmpty()) {
int[] record = heap.poll();
int x = record[0];
int y = record[1];
int c = record[2];
if (visited[x][y]) {
continue;
}
if (x == n - 1 && y == m - 1) {
return c;
}
visited[x][y] = true;
for (int i = 0; i < 4; i++) {
int nx = x + move[i];
int ny = y + move[i + 1];
if (nx >= 0 && nx < n && ny >= 0 && ny < m && !visited[nx][ny]) {
int nc = Math.max(c, Math.abs(heights[x][y] - heights[nx][ny]));
if (nc < distance[nx][ny]) {
distance[nx][ny] = nc;
heap.add(new int[]{nx, ny, nc});
}
}
}
}
return -1;
}
}java
class Solution {
public static int[] move = new int[]{-1, 0, 1, 0, -1};
public int swimInWater(int[][] grid) {
int n = grid.length;
int m = grid[0].length;
int[][] distance = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
distance[i][j] = Integer.MAX_VALUE;
}
}
distance[0][0] = 0;
boolean[][] visited = new boolean[n][m];
PriorityQueue<int[]> heap = new PriorityQueue<>((a, b) -> a[2] - b[2]);
heap.add(new int[]{0, 0, grid[0][0]});
while (!heap.isEmpty()) {
int x = heap.peek()[0];
int y = heap.peek()[1];
int c = heap.peek()[2];
heap.poll();
if (visited[x][y]) {
continue;
}
visited[x][y] = true;
if (x == n - 1 && y == m - 1) {
return c;
}
for (int i = 0; i < 4; i++) {
int nx = x + move[i];
int ny = y + move[i + 1];
if (nx >= 0 && nx < n && ny >= 0 && ny < m && !visited[nx][ny]) {
int nc = Math.max(c, grid[nx][ny]);
if (nc < distance[nx][ny]) {
distance[nx][ny] = nc;
heap.add(new int[]{nx, ny, nc});
}
}
}
}
return -1;
}
}A* 算法
IMPORTANT
A* 算法，指定源点，指定目标点，求源点到达目标点的最短距离
增加了当前点到终点的预估函数
在堆中根据 从源点出发到达当前点的距离+当前点到终点的预估距离 来进行排序
剩下的所有细节和 Dijskra 算法完全一致
预估函数要求：当前点到终点的预估距离 <= 当前点到终点的真实最短距离 预估函数是一种吸引力 1）合适的吸引力可以提升算法的速度，吸引力过强会出现错误 2）保证 预估距离 <= 真实最短距离 的情况下，尽量接近真实最短距离，可以做到功能正确 且 最快
预估终点距离经常选择： 曼哈顿距离欧式距离对角线距离
A* 模板
java
public class Solution {
public static int[] move = new int[] {-1, 0, 1, 0, -1};
public static int minDistance(int[][] grid, int startX, int startY, int targetX, int targetY) {
if (grid[startX][startY] == 0 || grid[targetX][targetY] == 0) {
return -1;
}
int n = grid.length;
int m = grid[0].length;
int[][] distance = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
distance[i][j] = Integer.MAX_VALUE;
}
}
distance[startX][startY] = 1;
boolean[] visited = new boolean[n][m];
PriorityQueue<int[]> heap = new PriorityQueue<>((a, b) -> a[2] - b[2]);
heap.add(new int[]{startX, startY, 1 + f1(startX, startY, targetX, targetY)});
while (!heap.isEmpty()) {
int[] cur = heap.poll();
int x = cur[0];
int y = cur[1];
if (visited[x][y]) {
continue;
}
visited[x][y] = true;
if (x == targetX && y == targetY) {
return distance[x][y];
}
for (int i = 0; i < 4; i++) {
let nx = x + move[i];
let ny = y + move[i + 1];
if (nx >= 0 && nx < n && ny >= 0 && ny < m
&& grid[nx][ny] == 1
&& !visited[nx])[ny]
&& distance[x][y] + 1 < distance[nx][ny]) {
distance[nx][ny] = distance[x][y] + 1;
heap.add(new int[]{nx, ny, distance[x][y] + 1 + f1(nx, ny, targetX, targetY)});
}
}
}
return -1;
}
}
// 曼哈顿距离
public static int f1(int x, int y, int targetX, int targetY) {
return (Math.abs(targetX - x) + Math.abs(targetY - y));
}
// 对角线距离
public static int f2(int x, int y, int targetX, int targetY) {
return Math.max(Math.abs(targetX - x), Math.abs(targetY - y));
}
// 欧式距离
public static double f3(int x, int y, int targetX, int targetY) {
return Math.sqrt(Math.pow(targetX - x, 2) + Math.pow(targetY - y, 2));
}Floyd 算法
IMPORTANT
Floyd 算法，得到图中任意两点之间的最短距离
时间复杂度 O(n^3)，空间复杂度 O(n^2)，常数时间小，容易实现
适用于任何图，不管有向无向、不管边权正负、但是不能有负环（保证最短路存在）
过程简述:
distance[i][j] 表示 i 和 j 之间的最短距离
distance[i][j] = min ( distance[i][j] , distance[i][k] + distance[k][j])
枚举所有的 k 即可，实现时一定要最先枚举跳板！
java
public class Sloution {
public static int MAXN = 101;
public static int MAXM = 10001;
public static int[] path = new int[MAXM];
public static int[][] distance = new int[MAXN][MAXM];
public static int n, m, ans;
// 初始时设置任意两点之间的最短距离为无穷大，表示任何路不存在
public static void build() {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
distance[i][j] = Integer.MAX_VALUE;
}
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in = new StreamTokenizer(br);
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
while (in.nextToken() != StreamTokenizer.TT_EOF) {
n = (int) in.nval;
in.nextToken();
m = (int) in.nval;
for (int i = 0; i < m; i++) {
in.nextToken();
path[i] = (int) in.nval - 1;
}
// 这道题给的图是邻接矩阵的形式
// 任意两点之间的边权都会给定
// 所以显得distance初始化不太必要
// 但是一般情况下，distance初始化一定要做
build();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
in.nextToken();
distance[i][j] = (int) in.nval;
}
}
floyd();
ans = 0;
for (int i = 1; i < m; i++) {
ans += distance[path[i - 1]][path[i]];
}
out.println(ans);
}
out.flush();
out.close();
br.close();
}
public static void floyd() {
// O(N^3)的过程
// 枚举每个跳板
// 注意，跳板要最先枚举！跳板要最先枚举！跳板要最先枚举！
for (int bridge = 0; bridge < n; bridge++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
// i -> .....bridge .... -> j
// distance[i][j]能不能缩短
// distance[i][j] = min ( distance[i][j] , distance[i][bridge] + distance[bridge][j])
if (distance[i][bridge] != Integer.MAX_VALUE
&& distance[bridge][j] != Integer.MAX_VALUE
&& distance[i][j] > distance[i][bridge] + distance[bridge][j]) {
distance[i][j] = distance[i][bridge] + distance[bridge][j];
}
}
}
}
}
}一维动态规划
斐波那契数列问题
IMPORTANT
动态规划的大致过程：
想出设计优良的递归尝试(方法、经验、固定套路很多)，有关尝试展开顺序的说明
-> 记忆化搜索(从顶到底的动态规划) ，如果每个状态的计算枚举代价很低，往往到这里就可以了
-> 严格位置依赖的动态规划(从底到顶的动态规划) ，更多是为了下面说的 进一步优化枚举做的准备
-> 进一步优化空间（空间压缩），一维、二维、多维动态规划都存在这种优化
-> 进一步优化枚举也就是优化时间（本节没有涉及，但是后续巨多内容和这有关）
1. 暴力递归
IMPORTANT
时间复杂度 O(2^n)
自顶向下的动态规划
js
const fib = (n) => {
if (n === 0) {
return 0;
}
if (n === 1) {
return 1;
}
return fib(n - 1) + fib(n - 2);
}2. 记忆化搜索
IMPORTANT
时间复杂度 O(n)
自顶向下的动态规划
js
const f = (n) => {
let dp = Array.from({length: n + 1}, () => -1);
return f(n, dp);
}
const fib = (i, dp) => {
if (i === 0) {
return 0;
}
if (i === 1) {
return 1;
}
if (dp[i] !== -1) {
return dp[i];
}
let ans = fib(i - 1, dp) + fib(i - 2, dp);
dp[i] = ans;
return ans;
}3. 自底向上的动态规划
IMPORTANT
自底向上的动态规划
js
const fib = (n) => {
if (n === 0) {
return 0;
}
if (n === 1) {
return 1;
}
let dp = Array.from({length: n + 1}, () => 0);
dp[1] = 1;
for (let i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}4. 常数空间的自底向上的动态规划
IMPORTANT
自底向上的动态规划
js
const fib = (n) => {
if (n === 0) {
return 0;
}
if (n === 1) {
return 1;
}
let lastlast = 0, last = 1;
for (let i = 2; i <= n; i++) {
let cur = lastlast + last;
lastlast = last;
last = cur;
}
return last;
}最低票价问题
1. 暴力递归（超出时间限制）
js
const durations = [1, 7, 30];
var mincostTickets = function(days, costs) {
return f(days, costs, 0);
};
const f = (days, costs, i) => {
if (i === days.length) {
return 0;
}
let ans = Number.MAX_VALUE;
for (let k = 0, j = i; k < 3; k++) {
while (j < days.length && days[i] + durations[k] > days[j]) {
j++;
}
ans = Math.min(ans, costs[k] + f(days, costs, j));
}
return ans;
}2. 记忆化搜索
js
const durations = [1, 7, 30];
var mincostTickets = function(days, costs) {
let dp = Array.from({length: days.length + 1}, () => Number.MAX_VALUE);
return f(days, costs, 0, dp);
};
const f = (days, costs, i, dp) => {
if (i === days.length) {
return 0;
}
if (dp[i] !== Number.MAX_VALUE) {
return dp[i];
}
let ans = Number.MAX_VALUE;
for (let k = 0, j = i; k < 3; k++) {
while (j < days.length && days[i] + durations[k] > days[j]) {
j++;
}
ans = Math.min(ans, costs[k] + f(days, costs, j, dp));
}
dp[i] = ans;
return ans;
}3. 自底向上的动态规划
IMPORTANT
我们可以看到状态转移方程其实就是尝试策略
js
while (j < days.length && days[i] + durations[k] > days[j]) {
j++;
}
ans = Math.min(ans, costs[k] + f(days, costs, j, dp));js
const durations = [1, 7, 30];
var mincostTickets = function(days, costs) {
let n = days.length;
let dp = Array.from({length: n + 1}, () => Number.MAX_VALUE);
// 初始化 dp[n]
dp[n] = 0;
for (let i = n - 1; i >= 0; i--) {
for (let k = 0, j = i; k < 3; k++) {
while (j < n && days[i] + durations[k] > days[j]) {
j++;
}
dp[i] = Math.min(dp[i], costs[k] + dp[j]);
}
}
return dp[0];
};解码方法
js
var numDecodings = function(s) {
let n = s.length;
let dp = Array.from({length: n + 1}, () => 0);
dp[n] = 1;
for (let i = n - 1; i >= 0; i--) {
if (s[i] === '0') {
dp[i] = 0;
} else {
dp[i] = dp[i + 1];
if (i + 1 < n && ((s[i].charCodeAt() - '0'.charCodeAt()) * 10 + s[i + 1].charCodeAt() - '0'.charCodeAt()) <= 26) {
dp[i] += dp[i + 2];
}
}
}
return dp[0];
};解码方法Ⅱ
java
public class Code04_DecodeWaysII {
// 没有取模逻辑
// 最自然的暴力尝试
public static int numDecodings1(String str) {
return f1(str.toCharArray(), 0);
}
// s[i....] 有多少种有效转化
public static int f1(char[] s, int i) {
if (i == s.length) {
return 1;
}
if (s[i] == '0') {
return 0;
}
// s[i] != '0'
// 2) i想单独转
int ans = f1(s, i + 1) * (s[i] == '*' ? 9 : 1);
// 3) i i+1 一起转化 <= 26
if (i + 1 < s.length) {
// 有i+1位置
if (s[i] != '*') {
if (s[i + 1] != '*') {
// num num
// i i+1
if ((s[i] - '0') * 10 + s[i + 1] - '0' <= 26) {
ans += f1(s, i + 2);
}
} else {
// num *
// i i+1
if (s[i] == '1') {
ans += f1(s, i + 2) * 9;
}
if (s[i] == '2') {
ans += f1(s, i + 2) * 6;
}
}
} else {
if (s[i + 1] != '*') {
// * num
// i i+1
if (s[i + 1] <= '6') {
ans += f1(s, i + 2) * 2;
} else {
ans += f1(s, i + 2);
}
} else {
// * *
// i i+1
// 11 12 ... 19 21 22 ... 26 -> 一共15种可能
// 没有10、20，因为*只能变1~9，并不包括0
ans += f1(s, i + 2) * 15;
}
}
}
return ans;
}
public static long mod = 1000000007;
public static int numDecodings2(String str) {
char[] s = str.toCharArray();
long[] dp = new long[s.length];
Arrays.fill(dp, -1);
return (int) f2(s, 0, dp);
}
public static long f2(char[] s, int i, long[] dp) {
if (i == s.length) {
return 1;
}
if (s[i] == '0') {
return 0;
}
if (dp[i] != -1) {
return dp[i];
}
long ans = f2(s, i + 1, dp) * (s[i] == '*' ? 9 : 1);
if (i + 1 < s.length) {
if (s[i] != '*') {
if (s[i + 1] != '*') {
if ((s[i] - '0') * 10 + s[i + 1] - '0' <= 26) {
ans += f2(s, i + 2, dp);
}
} else {
if (s[i] == '1') {
ans += f2(s, i + 2, dp) * 9;
}
if (s[i] == '2') {
ans += f2(s, i + 2, dp) * 6;
}
}
} else {
if (s[i + 1] != '*') {
if (s[i + 1] <= '6') {
ans += f2(s, i + 2, dp) * 2;
} else {
ans += f2(s, i + 2, dp);
}
} else {
ans += f2(s, i + 2, dp) * 15;
}
}
}
ans %= mod;
dp[i] = ans;
return ans;
}
public static int numDecodings3(String str) {
char[] s = str.toCharArray();
int n = s.length;
long[] dp = new long[n + 1];
dp[n] = 1;
for (int i = n - 1; i >= 0; i--) {
if (s[i] != '0') {
dp[i] = (s[i] == '*' ? 9 : 1) * dp[i + 1];
if (i + 1 < n) {
if (s[i] != '*') {
if (s[i + 1] != '*') {
if ((s[i] - '0') * 10 + s[i + 1] - '0' <= 26) {
dp[i] += dp[i + 2];
}
} else {
if (s[i] == '1') {
dp[i] += dp[i + 2] * 9;
}
if (s[i] == '2') {
dp[i] += dp[i + 2] * 6;
}
}
} else {
if (s[i + 1] != '*') {
if (s[i + 1] <= '6') {
dp[i] += dp[i + 2] * 2;
} else {
dp[i] += dp[i + 2];
}
} else {
dp[i] += dp[i + 2] * 15;
}
}
}
dp[i] %= mod;
}
}
return (int) dp[0];
}
public static int numDecodings4(String str) {
char[] s = str.toCharArray();
int n = s.length;
long cur = 0, next = 1, nextNext = 0;
for (int i = n - 1; i >= 0; i--) {
if (s[i] != '0') {
cur = (s[i] == '*' ? 9 : 1) * next;
if (i + 1 < n) {
if (s[i] != '*') {
if (s[i + 1] != '*') {
if ((s[i] - '0') * 10 + s[i + 1] - '0' <= 26) {
cur += nextNext;
}
} else {
if (s[i] == '1') {
cur += nextNext * 9;
}
if (s[i] == '2') {
cur += nextNext * 6;
}
}
} else {
if (s[i + 1] != '*') {
if (s[i + 1] <= '6') {
cur += nextNext * 2;
} else {
cur += nextNext;
}
} else {
cur += nextNext * 15;
}
}
}
cur %= mod;
}
nextNext = next;
next = cur;
cur = 0;
}
return (int) next;
}
}丑数Ⅱ
java
public class Code05_UglyNumberII {
// 时间复杂度O(n)，n代表第n个丑数
public static int nthUglyNumber(int n) {
// dp 0 1 2 ... n
// 1 2 ... ?
int[] dp = new int[n + 1];
dp[1] = 1;
for (int i = 2, i2 = 1, i3 = 1, i5 = 1, a, b, c, cur; i <= n; i++) {
a = dp[i2] * 2;
b = dp[i3] * 3;
c = dp[i5] * 5;
cur = Math.min(Math.min(a, b), c);
if (cur == a) {
i2++;
}
if (cur == b) {
i3++;
}
if (cur == c) {
i5++;
}
dp[i] = cur;
}
return dp[n];
}
}最长有效括号
java
public class Code06_LongestValidParentheses {
// 时间复杂度O(n)，n是str字符串的长度
public static int longestValidParentheses(String str) {
char[] s = str.toCharArray();
// dp[0...n-1]
// dp[i] : 子串必须以i位置的字符结尾的情况下，往左整体有效的最大长度
int[] dp = new int[s.length];
int ans = 0;
for (int i = 1, p; i < s.length; i++) {
if (s[i] == ')') {
p = i - dp[i - 1] - 1;
// ? )
// p i
if (p >= 0 && s[p] == '(') {
dp[i] = dp[i - 1] + 2 + (p - 1 >= 0 ? dp[p - 1] : 0);
}
}
ans = Math.max(ans, dp[i]);
}
return ans;
}
}环绕字符串中唯一的子字符串
java
public class Code07_UniqueSubstringsWraparoundString {
// 时间复杂度O(n)，n是字符串s的长度，字符串base长度为正无穷
public static int findSubstringInWraproundString(String str) {
int n = str.length();
int[] s = new int[n];
// abcde...z -> 0, 1, 2, 3, 4....25
for (int i = 0; i < n; i++) {
s[i] = str.charAt(i) - 'a';
}
// dp[0] : s中必须以'a'的子串，最大延伸长度是多少，延伸一定要跟据base串的规则
int[] dp = new int[26];
// s : c d e....
// 2 3 4
dp[s[0]] = 1;
for (int i = 1, cur, pre, len = 1; i < n; i++) {
cur = s[i];
pre = s[i - 1];
// pre cur
if ((pre == 25 && cur == 0) || pre + 1 == cur) {
// (前一个字符是'z' && 当前字符是'a') || 前一个字符比当前字符的ascii码少1
len++;
} else {
len = 1;
}
dp[cur] = Math.max(dp[cur], len);
}
int ans = 0;
for (int i = 0; i < 26; i++) {
ans += dp[i];
}
return ans;
}
}不同的子序列 II
java
public class Code08_DistinctSubsequencesII {
// 时间复杂度O(n)，n是字符串s的长度
public static int distinctSubseqII(String s) {
int mod = 1000000007;
char[] str = s.toCharArray();
int[] cnt = new int[26];
int all = 1, newAdd;
for (char x : str) {
newAdd = (all - cnt[x - 'a'] + mod) % mod;
cnt[x - 'a'] = (cnt[x - 'a'] + newAdd) % mod;
all = (all + newAdd) % mod;
}
return (all - 1 + mod) % mod;
}
}二维动态规划
IMPORTANT
尝试函数有 1 个可变参数可以完全决定返回值，进而可以改出1维动态规划表的实现
同理
尝试函数有 2 个可变参数可以完全决定返回值，那么就可以改出2维动态规划的实现
一维、二维、三维甚至多维动态规划问题，大体过程都是：
写出尝试递归
记忆化搜索(从顶到底的动态规划)
严格位置依赖的动态规划(从底到顶的动态规划)
空间、时间的更多优化
二维动态规划依然需要去整理 动态规划表的格子之间的依赖关系 找寻依赖关系，往往 通过画图来建立空间感，使其更显而易见 然后依然是 从简单格子填写到复杂格子 的过程，即严格位置依赖的动态规划(从底到顶)
二维动态规划的压缩空间技巧原理不难，会了之后千篇一律 但是不同题目依赖关系不一样，需要 很细心的画图来整理具体题目的依赖关系 最后进行空间压缩的实现
能改成动态规划的递归，统一特征： 决定返回值的可变参数类型往往都比较简单，一般不会比 int 类型更复杂。为什么？
从这个角度，可以解释 带路径的递归（可变参数类型复杂），不适合或者说没有必要改成动态规划 题目 2 就是说明这一点的
一定要 写出可变参数类型简单（不比 int 类型更复杂），并且 可以完全决定返回值的递归， 保证做到 这些可变参数可以完全代表之前决策过程对后续过程的影响！再去改动态规划！
不管几维动态规划 经常从递归的定义出发，避免后续进行很多边界讨论 这需要一定的经验来预知
最小路径和
java
public class Code01_MinimumPathSum {
// 暴力递归
public static int minPathSum1(int[][] grid) {
return f1(grid, grid.length - 1, grid[0].length - 1);
}
// 从(0,0)到(i,j)最小路径和
// 一定每次只能向右或者向下
public static int f1(int[][] grid, int i, int j) {
if (i == 0 && j == 0) {
return grid[0][0];
}
int up = Integer.MAX_VALUE;
int left = Integer.MAX_VALUE;
if (i - 1 >= 0) {
up = f1(grid, i - 1, j);
}
if (j - 1 >= 0) {
left = f1(grid, i, j - 1);
}
return grid[i][j] + Math.min(up, left);
}
// 记忆化搜索
public static int minPathSum2(int[][] grid) {
int n = grid.length;
int m = grid[0].length;
int[][] dp = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
dp[i][j] = -1;
}
}
return f2(grid, grid.length - 1, grid[0].length - 1, dp);
}
public static int f2(int[][] grid, int i, int j, int[][] dp) {
if (dp[i][j] != -1) {
return dp[i][j];
}
int ans;
if (i == 0 && j == 0) {
ans = grid[0][0];
} else {
int up = Integer.MAX_VALUE;
int left = Integer.MAX_VALUE;
if (i - 1 >= 0) {
up = f2(grid, i - 1, j, dp);
}
if (j - 1 >= 0) {
left = f2(grid, i, j - 1, dp);
}
ans = grid[i][j] + Math.min(up, left);
}
dp[i][j] = ans;
return ans;
}
// 严格位置依赖的动态规划
public static int minPathSum3(int[][] grid) {
int n = grid.length;
int m = grid[0].length;
int[][] dp = new int[n][m];
dp[0][0] = grid[0][0];
for (int i = 1; i < n; i++) {
dp[i][0] = dp[i - 1][0] + grid[i][0];
}
for (int j = 1; j < m; j++) {
dp[0][j] = dp[0][j - 1] + grid[0][j];
}
for (int i = 1; i < n; i++) {
for (int j = 1; j < m; j++) {
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
}
}
return dp[n - 1][m - 1];
}
// 严格位置依赖的动态规划 + 空间压缩技巧
public static int minPathSum4(int[][] grid) {
int n = grid.length;
int m = grid[0].length;
// 先让dp表，变成想象中的表的第0行的数据
int[] dp = new int[m];
dp[0] = grid[0][0];
for (int j = 1; j < m; j++) {
dp[j] = dp[j - 1] + grid[0][j];
}
for (int i = 1; i < n; i++) {
// i = 1，dp表变成想象中二维表的第1行的数据
// i = 2，dp表变成想象中二维表的第2行的数据
// i = 3，dp表变成想象中二维表的第3行的数据
// ...
// i = n-1，dp表变成想象中二维表的第n-1行的数据
dp[0] += grid[i][0];
for (int j = 1; j < m; j++) {
dp[j] = Math.min(dp[j - 1], dp[j]) + grid[i][j];
}
}
return dp[m - 1];
}
}单词搜索（无法改成动态规划）
java
public class Code02_WordSearch {
public static boolean exist(char[][] board, String word) {
char[] w = word.toCharArray();
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
if (f(board, i, j, w, 0)) {
return true;
}
}
}
return false;
}
// 因为board会改其中的字符
// 用来标记哪些字符无法再用
// 带路径的递归无法改成动态规划或者说没必要
// 从(i,j)出发，来到w[k]，请问后续能不能把word走出来w[k...]
public static boolean f(char[][] b, int i, int j, char[] w, int k) {
if (k == w.length) {
return true;
}
if (i < 0 || i == b.length || j < 0 || j == b[0].length || b[i][j] != w[k]) {
return false;
}
// 不越界，b[i][j] == w[k]
char tmp = b[i][j];
b[i][j] = 0;
boolean ans = f(b, i - 1, j, w, k + 1)
|| f(b, i + 1, j, w, k + 1)
|| f(b, i, j - 1, w, k + 1)
|| f(b, i, j + 1, w, k + 1);
b[i][j] = tmp;
return ans;
}
}最长公共子序列
java
public class Code03_LongestCommonSubsequence {
public static int longestCommonSubsequence1(String str1, String str2) {
char[] s1 = str1.toCharArray();
char[] s2 = str2.toCharArray();
int n = s1.length;
int m = s2.length;
return f1(s1, s2, n - 1, m - 1);
}
// s1[0....i1]与s2[0....i2]最长公共子序列长度
public static int f1(char[] s1, char[] s2, int i1, int i2) {
if (i1 < 0 || i2 < 0) {
return 0;
}
int p1 = f1(s1, s2, i1 - 1, i2 - 1);
int p2 = f1(s1, s2, i1 - 1, i2);
int p3 = f1(s1, s2, i1, i2 - 1);
int p4 = s1[i1] == s2[i2] ? (p1 + 1) : 0;
return Math.max(Math.max(p1, p2), Math.max(p3, p4));
}
// 为了避免很多边界讨论
// 很多时候往往不用下标来定义尝试，而是用长度来定义尝试
// 因为长度最短是0，而下标越界的话讨论起来就比较麻烦
public static int longestCommonSubsequence2(String str1, String str2) {
char[] s1 = str1.toCharArray();
char[] s2 = str2.toCharArray();
int n = s1.length;
int m = s2.length;
return f2(s1, s2, n, m);
}
// s1[前缀长度为len1]对应s2[前缀长度为len2]
// 最长公共子序列长度
public static int f2(char[] s1, char[] s2, int len1, int len2) {
if (len1 == 0 || len2 == 0) {
return 0;
}
int ans;
if (s1[len1 - 1] == s2[len2 - 1]) {
ans = f2(s1, s2, len1 - 1, len2 - 1) + 1;
} else {
ans = Math.max(f2(s1, s2, len1 - 1, len2), f2(s1, s2, len1, len2 - 1));
}
return ans;
}
// 记忆化搜索
public static int longestCommonSubsequence3(String str1, String str2) {
char[] s1 = str1.toCharArray();
char[] s2 = str2.toCharArray();
int n = s1.length;
int m = s2.length;
int[][] dp = new int[n + 1][m + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= m; j++) {
dp[i][j] = -1;
}
}
return f3(s1, s2, n, m, dp);
}
public static int f3(char[] s1, char[] s2, int len1, int len2, int[][] dp) {
if (len1 == 0 || len2 == 0) {
return 0;
}
if (dp[len1][len2] != -1) {
return dp[len1][len2];
}
int ans;
if (s1[len1 - 1] == s2[len2 - 1]) {
ans = f3(s1, s2, len1 - 1, len2 - 1, dp) + 1;
} else {
ans = Math.max(f3(s1, s2, len1 - 1, len2, dp), f3(s1, s2, len1, len2 - 1, dp));
}
dp[len1][len2] = ans;
return ans;
}
// 严格位置依赖的动态规划
public static int longestCommonSubsequence4(String str1, String str2) {
char[] s1 = str1.toCharArray();
char[] s2 = str2.toCharArray();
int n = s1.length;
int m = s2.length;
int[][] dp = new int[n + 1][m + 1];
for (int len1 = 1; len1 <= n; len1++) {
for (int len2 = 1; len2 <= m; len2++) {
if (s1[len1 - 1] == s2[len2 - 1]) {
dp[len1][len2] = 1 + dp[len1 - 1][len2 - 1];
} else {
dp[len1][len2] = Math.max(dp[len1 - 1][len2], dp[len1][len2 - 1]);
}
}
}
return dp[n][m];
}
// 严格位置依赖的动态规划 + 空间压缩
public static int longestCommonSubsequence5(String str1, String str2) {
char[] s1, s2;
if (str1.length() >= str2.length()) {
s1 = str1.toCharArray();
s2 = str2.toCharArray();
} else {
s1 = str2.toCharArray();
s2 = str1.toCharArray();
}
int n = s1.length;
int m = s2.length;
int[] dp = new int[m + 1];
for (int len1 = 1; len1 <= n; len1++) {
int leftUp = 0, backup;
for (int len2 = 1; len2 <= m; len2++) {
backup = dp[len2];
if (s1[len1 - 1] == s2[len2 - 1]) {
dp[len2] = 1 + leftUp;
} else {
dp[len2] = Math.max(dp[len2], dp[len2 - 1]);
}
leftUp = backup;
}
}
return dp[m];
}
}最长公共子序列Ⅱ
TIP
与最长公共子序列的不同之处在于：最长公共子序列是让求长度，最长公共子序列Ⅱ是求出该最长公共子序列的字符串
js
function LCS( s1 , s2 ) {
// write code here
if (s1 === '' || s2 === '') return "-1";
let n = s1.length;
let m = s2.length;
// dp[i][j]：表示以 s1 以第 i 个字符结尾且 s2 以第 j 个字符结尾的最长公共子序列的长度
let dp = Array.from({length: n + 1}, () => Array.from({length: m + 1}, () => ""));
for (let i = 1; i <= n; i++) {
let pre = '';
for (let j = 1; j <= m; j++) {
const tmp = dp[i - 1][j];
if (s1[i - 1] === s2[j - 1]) {
dp[i][j] = pre + s2[j - 1];
} else {
dp[i][j] = dp[i - 1][j].length > dp[i][j - 1].length ? dp[i - 1][j] : dp[i][j - 1];
}
pre = tmp;
}
}
let res = dp[n][m];
return res === '' ? "-1" : res;
}最长公共子串
TIP
定义**dp[i][j]表示字符串str1中第i个字符和str2种第j个字符为最后一个元素所构成的最长公共子串**。如果要求dp[i][j]，也就是 str1 的第 i 个字符和 str2 的第 j 个字符为最后一个元素所构成的最长公共子串，我们首先需要判断这两个字符是否相等。
- 如果不相等，那么他们就不能构成公共子串，也就是
dp[i][j]=0; - 如果相等，我们还需要计算前面相等字符的个数，其实就是
dp[i-1][j-1]，所以dp[i][j]=dp[i-1][j-1]+1;
js
function LCS( str1 , str2 ) {
// write code here
if (str1 === '' || str2 === '') {
return "";
}
let n = str1.length;
let m = str2.length;
let dp = Array.from({length: n + 1}, () => Array.from({length: m + 1}, () => 0));
let maxLength = 0, maxIndex = 0;
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= m; j++) {
if (str1[i - 1] === str2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
if (dp[i][j] > maxLength) {
maxLength = dp[i][j];
maxIndex = i - 1;
}
} else {
dp[i][j] = 0;
}
}
}
return str1.substring(maxIndex - maxLength + 1, maxIndex + 1);
}最长回文子序列
java
public class Code04_LongestPalindromicSubsequence {
// 最长回文子序列问题可以转化成最长公共子序列问题
// 不过这里讲述区间动态规划的思路
// 区间dp还会有单独的视频做详细讲述
public static int longestPalindromeSubseq1(String str) {
char[] s = str.toCharArray();
int n = s.length;
return f1(s, 0, n - 1);
}
// s[l...r]最长回文子序列长度
// l <= r
public static int f1(char[] s, int l, int r) {
if (l == r) {
return 1;
}
if (l + 1 == r) {
return s[l] == s[r] ? 2 : 1;
}
if (s[l] == s[r]) {
return 2 + f1(s, l + 1, r - 1);
} else {
return Math.max(f1(s, l + 1, r), f1(s, l, r - 1));
}
}
public static int longestPalindromeSubseq2(String str) {
char[] s = str.toCharArray();
int n = s.length;
int[][] dp = new int[n][n];
return f2(s, 0, n - 1, dp);
}
public static int f2(char[] s, int l, int r, int[][] dp) {
if (l == r) {
return 1;
}
if (l + 1 == r) {
return s[l] == s[r] ? 2 : 1;
}
if (dp[l][r] != 0) {
return dp[l][r];
}
int ans;
if (s[l] == s[r]) {
ans = 2 + f2(s, l + 1, r - 1, dp);
} else {
ans = Math.max(f2(s, l + 1, r, dp), f2(s, l, r - 1, dp));
}
dp[l][r] = ans;
return ans;
}
public static int longestPalindromeSubseq3(String str) {
char[] s = str.toCharArray();
int n = s.length;
int[][] dp = new int[n][n];
for (int l = n - 1; l >= 0; l--) {
dp[l][l] = 1;
if (l + 1 < n) {
dp[l][l + 1] = s[l] == s[l + 1] ? 2 : 1;
}
for (int r = l + 2; r < n; r++) {
if (s[l] == s[r]) {
dp[l][r] = 2 + dp[l + 1][r - 1];
} else {
dp[l][r] = Math.max(dp[l + 1][r], dp[l][r - 1]);
}
}
}
return dp[0][n - 1];
}
public static int longestPalindromeSubseq4(String str) {
char[] s = str.toCharArray();
int n = s.length;
int[] dp = new int[n];
for (int l = n - 1, leftDown = 0, backup; l >= 0; l--) {
// dp[l] : 想象中的dp[l][l]
dp[l] = 1;
if (l + 1 < n) {
leftDown = dp[l + 1];
// dp[l+1] : 想象中的dp[l][l+1]
dp[l + 1] = s[l] == s[l + 1] ? 2 : 1;
}
for (int r = l + 2; r < n; r++) {
backup = dp[r];
if (s[l] == s[r]) {
dp[r] = 2 + leftDown;
} else {
dp[r] = Math.max(dp[r], dp[r - 1]);
}
leftDown = backup;
}
}
return dp[n - 1];
}
}节点数为n高度不大于m的二叉树个数
java
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
public class Code05_NodenHeightNotLargerThanm {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in = new StreamTokenizer(br);
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
while (in.nextToken() != StreamTokenizer.TT_EOF) {
int n = (int) in.nval;
in.nextToken();
int m = (int) in.nval;
out.println(compute3(n, m));
}
out.flush();
out.close();
br.close();
}
public static int MAXN = 51;
public static int MOD = 1000000007;
// 记忆化搜索
public static long[][] dp1 = new long[MAXN][MAXN];
static {
for (int i = 0; i < MAXN; i++) {
for (int j = 0; j < MAXN; j++) {
dp1[i][j] = -1;
}
}
}
// 二叉树节点数为n
// 高度不能超过m
// 结构数返回
// 记忆化搜索
public static int compute1(int n, int m) {
if (n == 0) {
return 1;
}
// n > 0
if (m == 0) {
return 0;
}
if (dp1[n][m] != -1) {
return (int) dp1[n][m];
}
long ans = 0;
// n个点，头占掉1个
for (int k = 0; k < n; k++) {
// 一共n个节点，头节点已经占用了1个名额
// 如果左树占用k个，那么右树就占用i-k-1个
ans = (ans + ((long) compute1(k, m - 1) * compute1(n - k - 1, m - 1)) % MOD) % MOD;
}
dp1[n][m] = ans;
return (int) ans;
}
// 严格位置依赖的动态规划
public static long[][] dp2 = new long[MAXN][MAXN];
public static int compute2(int n, int m) {
for (int j = 0; j <= m; j++) {
dp2[0][j] = 1;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
dp2[i][j] = 0;
for (int k = 0; k < i; k++) {
// 一共i个节点，头节点已经占用了1个名额
// 如果左树占用k个，那么右树就占用i-k-1个
dp2[i][j] = (dp2[i][j] + dp2[k][j - 1] * dp2[i - k - 1][j - 1] % MOD) % MOD;
}
}
}
return (int) dp2[n][m];
}
// 空间压缩
public static long[] dp3 = new long[MAXN];
public static int compute3(int n, int m) {
dp3[0] = 1;
for (int i = 1; i <= n; i++) {
dp3[i] = 0;
}
for (int j = 1; j <= m; j++) {
// 根据依赖，一定要先枚举列
for (int i = n; i >= 1; i--) {
// 再枚举行，而且i不需要到达0，i>=1即可
dp3[i] = 0;
for (int k = 0; k < i; k++) {
// 枚举
dp3[i] = (dp3[i] + dp3[k] * dp3[i - k - 1] % MOD) % MOD;
}
}
}
return (int) dp3[n];
}
}矩阵中的最长递增路径
java
public class Code06_LongestIncreasingPath {
public static int longestIncreasingPath1(int[][] grid) {
int ans = 0;
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
ans = Math.max(ans, f1(grid, i, j));
}
}
return ans;
}
// 从(i,j)出发，能走出来多长的递增路径，返回最长长度
public static int f1(int[][] grid, int i, int j) {
int next = 0;
if (i > 0 && grid[i][j] < grid[i - 1][j]) {
next = Math.max(next, f1(grid, i - 1, j));
}
if (i + 1 < grid.length && grid[i][j] < grid[i + 1][j]) {
next = Math.max(next, f1(grid, i + 1, j));
}
if (j > 0 && grid[i][j] < grid[i][j - 1]) {
next = Math.max(next, f1(grid, i, j - 1));
}
if (j + 1 < grid[0].length && grid[i][j] < grid[i][j + 1]) {
next = Math.max(next, f1(grid, i, j + 1));
}
return next + 1;
}
public static int longestIncreasingPath2(int[][] grid) {
int n = grid.length;
int m = grid[0].length;
int[][] dp = new int[n][m];
int ans = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
ans = Math.max(ans, f2(grid, i, j, dp));
}
}
return ans;
}
public static int f2(int[][] grid, int i, int j, int[][] dp) {
if (dp[i][j] != 0) {
return dp[i][j];
}
int next = 0;
if (i > 0 && grid[i][j] < grid[i - 1][j]) {
next = Math.max(next, f2(grid, i - 1, j, dp));
}
if (i + 1 < grid.length && grid[i][j] < grid[i + 1][j]) {
next = Math.max(next, f2(grid, i + 1, j, dp));
}
if (j > 0 && grid[i][j] < grid[i][j - 1]) {
next = Math.max(next, f2(grid, i, j - 1, dp));
}
if (j + 1 < grid[0].length && grid[i][j] < grid[i][j + 1]) {
next = Math.max(next, f2(grid, i, j + 1, dp));
}
dp[i][j] = next + 1;
return next + 1;
}
}不同的子序列
java
package class068;
// 不同的子序列
// 给你两个字符串s和t ，统计并返回在s的子序列中t出现的个数
// 答案对 1000000007 取模
// 测试链接 : https://leetcode.cn/problems/distinct-subsequences/
public class Code01_DistinctSubsequences {
// 已经展示太多次从递归到动态规划了
// 直接写动态规划吧
public static int numDistinct1(String str, String target) {
char[] s = str.toCharArray();
char[] t = target.toCharArray();
int n = s.length;
int m = t.length;
// dp[i][j] :
// s[前缀长度为i]的所有子序列中，有多少个子序列等于t[前缀长度为j]
int[][] dp = new int[n + 1][m + 1];
for (int i = 0; i <= n; i++) {
dp[i][0] = 1;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
dp[i][j] = dp[i - 1][j];
if (s[i - 1] == t[j - 1]) {
dp[i][j] += dp[i - 1][j - 1];
}
}
}
return dp[n][m];
}
// 空间压缩
public static int numDistinct2(String str, String target) {
char[] s = str.toCharArray();
char[] t = target.toCharArray();
int n = s.length;
int m = t.length;
int[] dp = new int[m + 1];
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = m; j >= 1; j--) {
if (s[i - 1] == t[j - 1]) {
dp[j] += dp[j - 1];
}
}
}
return dp[m];
}
// 本题说了要取模，所以增加取模的逻辑
public static int numDistinct3(String str, String target) {
int mod = 1000000007;
char[] s = str.toCharArray();
char[] t = target.toCharArray();
int n = s.length;
int m = t.length;
int[] dp = new int[m + 1];
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = m; j >= 1; j--) {
if (s[i - 1] == t[j - 1]) {
dp[j] = (dp[j] + dp[j - 1]) % mod;
}
}
}
return dp[m];
}
}编辑距离
java
package class068;
// 编辑距离
// 给你两个单词 word1 和 word2
// 请返回将 word1 转换成 word2 所使用的最少代价
// 你可以对一个单词进行如下三种操作：
// 插入一个字符，代价a
// 删除一个字符，代价b
// 替换一个字符，代价c
// 测试链接 : https://leetcode.cn/problems/edit-distance/
public class Code02_EditDistance {
// 已经展示太多次从递归到动态规划了
// 直接写动态规划吧
public int minDistance(String word1, String word2) {
return editDistance2(word1, word2, 1, 1, 1);
}
// 原初尝试版
// a : str1中插入1个字符的代价
// b : str1中删除1个字符的代价
// c : str1中改变1个字符的代价
// 返回从str1转化成str2的最低代价
public static int editDistance1(String str1, String str2, int a, int b, int c) {
char[] s1 = str1.toCharArray();
char[] s2 = str2.toCharArray();
int n = s1.length;
int m = s2.length;
// dp[i][j] :
// s1[前缀长度为i]想变成s2[前缀长度为j]，至少付出多少代价
int[][] dp = new int[n + 1][m + 1];
for (int i = 1; i <= n; i++) {
dp[i][0] = i * b;
}
for (int j = 1; j <= m; j++) {
dp[0][j] = j * a;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
int p1 = Integer.MAX_VALUE;
if (s1[i - 1] == s2[j - 1]) {
p1 = dp[i - 1][j - 1];
}
int p2 = Integer.MAX_VALUE;
if (s1[i - 1] != s2[j - 1]) {
p2 = dp[i - 1][j - 1] + c;
}
int p3 = dp[i][j - 1] + a;
int p4 = dp[i - 1][j] + b;
dp[i][j] = Math.min(Math.min(p1, p2), Math.min(p3, p4));
}
}
return dp[n][m];
}
// 枚举小优化版
// a : str1中插入1个字符的代价
// b : str1中删除1个字符的代价
// c : str1中改变1个字符的代价
// 返回从str1转化成str2的最低代价
public static int editDistance2(String str1, String str2, int a, int b, int c) {
char[] s1 = str1.toCharArray();
char[] s2 = str2.toCharArray();
int n = s1.length;
int m = s2.length;
// dp[i][j] :
// s1[前缀长度为i]想变成s2[前缀长度为j]，至少付出多少代价
int[][] dp = new int[n + 1][m + 1];
for (int i = 1; i <= n; i++) {
dp[i][0] = i * b;
}
for (int j = 1; j <= m; j++) {
dp[0][j] = j * a;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (s1[i - 1] == s2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = Math.min(Math.min(dp[i - 1][j] + b, dp[i][j - 1] + a), dp[i - 1][j - 1] + c);
}
}
}
return dp[n][m];
}
// 空间压缩
public static int editDistance3(String str1, String str2, int a, int b, int c) {
char[] s1 = str1.toCharArray();
char[] s2 = str2.toCharArray();
int n = s1.length;
int m = s2.length;
int[] dp = new int[m + 1];
for (int j = 1; j <= m; j++) {
dp[j] = j * a;
}
for (int i = 1, leftUp, backUp; i <= n; i++) {
leftUp = (i - 1) * b;
dp[0] = i * b;
for (int j = 1; j <= m; j++) {
backUp = dp[j];
if (s1[i - 1] == s2[j - 1]) {
dp[j] = leftUp;
} else {
dp[j] = Math.min(Math.min(dp[j] + b, dp[j - 1] + a), leftUp + c);
}
leftUp = backUp;
}
}
return dp[m];
}
}交错字符串
java
package class068;
// 交错字符串
// 给定三个字符串 s1、s2、s3
// 请帮忙验证s3是否由s1和s2交错组成
// 测试链接 : https://leetcode.cn/problems/interleaving-string/
public class Code03_InterleavingString {
// 已经展示太多次从递归到动态规划了
// 直接写动态规划吧
public static boolean isInterleave1(String str1, String str2, String str3) {
if (str1.length() + str2.length() != str3.length()) {
return false;
}
char[] s1 = str1.toCharArray();
char[] s2 = str2.toCharArray();
char[] s3 = str3.toCharArray();
int n = s1.length;
int m = s2.length;
// dp[i][j]:
// s1[前缀长度为i]和s2[前缀长度为j]，能否交错组成出s3[前缀长度为i+j]
boolean[][] dp = new boolean[n + 1][m + 1];
dp[0][0] = true;
for (int i = 1; i <= n; i++) {
if (s1[i - 1] != s3[i - 1]) {
break;
}
dp[i][0] = true;
}
for (int j = 1; j <= m; j++) {
if (s2[j - 1] != s3[j - 1]) {
break;
}
dp[0][j] = true;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
dp[i][j] = (s1[i - 1] == s3[i + j - 1] && dp[i - 1][j]) || (s2[j - 1] == s3[i + j - 1] && dp[i][j - 1]);
}
}
return dp[n][m];
}
// 空间压缩
public static boolean isInterleave2(String str1, String str2, String str3) {
if (str1.length() + str2.length() != str3.length()) {
return false;
}
char[] s1 = str1.toCharArray();
char[] s2 = str2.toCharArray();
char[] s3 = str3.toCharArray();
int n = s1.length;
int m = s2.length;
boolean[] dp = new boolean[m + 1];
dp[0] = true;
for (int j = 1; j <= m; j++) {
if (s2[j - 1] != s3[j - 1]) {
break;
}
dp[j] = true;
}
for (int i = 1; i <= n; i++) {
dp[0] = s1[i - 1] == s3[i - 1] && dp[0];
for (int j = 1; j <= m; j++) {
dp[j] = (s1[i - 1] == s3[i + j - 1] && dp[j]) || (s2[j - 1] == s3[i + j - 1] && dp[j - 1]);
}
}
return dp[m];
}
}有效涂色问题
java
package class068;
import java.util.Arrays;
// 有效涂色问题
// 给定n、m两个参数
// 一共有n个格子，每个格子可以涂上一种颜色，颜色在m种里选
// 当涂满n个格子，并且m种颜色都使用了，叫一种有效方法
// 求一共有多少种有效的涂色方法
// 1 <= n, m <= 5000
// 结果比较大请 % 1000000007 之后返回
// 对数器验证
public class Code04_FillCellsUseAllColorsWays {
// 暴力方法
// 为了验证
public static int ways1(int n, int m) {
return f(new int[n], new boolean[m + 1], 0, n, m);
}
// 把所有填色的方法暴力枚举
// 然后一个一个验证是否有效
// 这是一个带路径的递归
// 无法改成动态规划
public static int f(int[] path, boolean[] set, int i, int n, int m) {
if (i == n) {
Arrays.fill(set, false);
int colors = 0;
for (int c : path) {
if (!set[c]) {
set[c] = true;
colors++;
}
}
return colors == m ? 1 : 0;
} else {
int ans = 0;
for (int j = 1; j <= m; j++) {
path[i] = j;
ans += f(path, set, i + 1, n, m);
}
return ans;
}
}
// 正式方法
// 时间复杂度O(n * m)
// 已经展示太多次从递归到动态规划了
// 直接写动态规划吧
// 也不做空间压缩了，因为千篇一律
// 有兴趣的同学自己试试
public static int MAXN = 5001;
public static int[][] dp = new int[MAXN][MAXN];
public static int mod = 1000000007;
public static int ways2(int n, int m) {
// dp[i][j]:
// 一共有m种颜色
// 前i个格子涂满j种颜色的方法数
for (int i = 1; i <= n; i++) {
dp[i][1] = m;
}
for (int i = 2; i <= n; i++) {
for (int j = 2; j <= m; j++) {
dp[i][j] = (int) (((long) dp[i - 1][j] * j) % mod);
dp[i][j] = (int) ((((long) dp[i - 1][j - 1] * (m - j + 1)) + dp[i][j]) % mod);
}
}
return dp[n][m];
}
public static void main(String[] args) {
// 测试的数据量比较小
// 那是因为数据量大了，暴力方法过不了
// 但是这个数据量足够说明正式方法是正确的
int N = 9;
int M = 9;
System.out.println("功能测试开始");
for (int n = 1; n <= N; n++) {
for (int m = 1; m <= M; m++) {
int ans1 = ways1(n, m);
int ans2 = ways2(n, m);
if (ans1 != ans2) {
System.out.println("出错了!");
}
}
}
System.out.println("功能测试结束");
System.out.println("性能测试开始");
int n = 5000;
int m = 4877;
System.out.println("n : " + n);
System.out.println("m : " + m);
long start = System.currentTimeMillis();
int ans = ways2(n, m);
long end = System.currentTimeMillis();
System.out.println("取模之后的结果 : " + ans);
System.out.println("运行时间 : " + (end - start) + " 毫秒");
System.out.println("性能测试结束");
}
}删除至少几个字符可以变成另一个字符串的子串
java
package class068;
import java.util.ArrayList;
import java.util.List;
// 删除至少几个字符可以变成另一个字符串的子串
// 给定两个字符串s1和s2
// 返回s1至少删除多少字符可以成为s2的子串
// 对数器验证
public class Code05_MinimumDeleteBecomeSubstring {
// 暴力方法
// 为了验证
public static int minDelete1(String s1, String s2) {
List<String> list = new ArrayList<>();
f(s1.toCharArray(), 0, "", list);
// 排序 : 长度大的子序列先考虑
// 因为如果长度大的子序列是s2的子串
// 那么需要删掉的字符数量 = s1的长度 - s1子序列长度
// 子序列长度越大，需要删掉的字符数量就越少
// 所以长度大的子序列先考虑
list.sort((a, b) -> b.length() - a.length());
for (String str : list) {
if (s2.indexOf(str) != -1) {
// 检查s2中，是否包含当前的s1子序列str
return s1.length() - str.length();
}
}
return s1.length();
}
// 生成s1字符串的所有子序列串
public static void f(char[] s1, int i, String path, List<String> list) {
if (i == s1.length) {
list.add(path);
} else {
f(s1, i + 1, path, list);
f(s1, i + 1, path + s1[i], list);
}
}
// 正式方法，动态规划
// 已经展示太多次从递归到动态规划了
// 直接写动态规划吧
// 也不做空间压缩了，因为千篇一律
// 有兴趣的同学自己试试
public static int minDelete2(String str1, String str2) {
char[] s1 = str1.toCharArray();
char[] s2 = str2.toCharArray();
int n = s1.length;
int m = s2.length;
// dp[len1][len2] :
// s1[前缀长度为i]至少删除多少字符，可以变成s2[前缀长度为j]的任意后缀串
int[][] dp = new int[n + 1][m + 1];
for (int i = 1; i <= n; i++) {
dp[i][0] = i;
for (int j = 1; j <= m; j++) {
if (s1[i - 1] == s2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = dp[i - 1][j] + 1;
}
}
}
int ans = Integer.MAX_VALUE;
for (int j = 0; j <= m; j++) {
ans = Math.min(ans, dp[n][j]);
}
return ans;
}
// 为了验证
// 生成长度为n，有v种字符的随机字符串
public static String randomString(int n, int v) {
char[] ans = new char[n];
for (int i = 0; i < n; i++) {
ans[i] = (char) ('a' + (int) (Math.random() * v));
}
return String.valueOf(ans);
}
// 为了验证
// 对数器
public static void main(String[] args) {
// 测试的数据量比较小
// 那是因为数据量大了，暴力方法过不了
// 但是这个数据量足够说明正式方法是正确的
int n = 12;
int v = 3;
int testTime = 20000;
System.out.println("测试开始");
for (int i = 0; i < testTime; i++) {
int len1 = (int) (Math.random() * n) + 1;
int len2 = (int) (Math.random() * n) + 1;
String s1 = randomString(len1, v);
String s2 = randomString(len2, v);
int ans1 = minDelete1(s1, s2);
int ans2 = minDelete2(s1, s2);
if (ans1 != ans2) {
System.out.println("出错了!");
}
}
System.out.println("测试结束");
}
}三维动态规划
一和零(多维费用背包)
js
let zeros, ones;
const zerosAndOnes = (str) => {
zeros = 0;
ones = 0;
for (let i = 0; i < str.length; i++) {
if (str[i] === '0') {
zeros++;
} else {
ones++;
}
}
}
var findMaxForm = function(strs, m, n) {
let dp = Array.from({length: strs.length}, () => Array.from({length: m + 1}, () => Array.from({length: n + 1}, () => -1)));
return f2(strs, 0, m, n, dp)
};
// const f1 = (strs, i, z, o) => {
// if (i === strs.length) {
// return 0;
// }
// // 不使用当前的strs[i]字符串
// let p1 = f1(strs, i + 1, z, o);
// // 使用当前的strs[i]字符串
// let p2 = 0;
// zerosAndOnes(strs[i]);
// if (zeros <= z && ones <= o) {
// p2 = 1 + f1(strs, i + 1, z - zeros, o - ones);
// }
// return Math.max(p1, p2);
// }
const f2 = (strs, i, z, o, dp) => {
if (i === strs.length) {
return 0;
}
if (dp[i][z][o] !== -1) {
return dp[i][z][o];
}
let p1 = f2(strs, i + 1, z, o, dp);
let p2 = 0;
zerosAndOnes(strs[i]);
if (zeros <= z && ones <= o) {
p2 = 1 + f2(strs, i + 1, z - zeros, o - ones, dp);
}
let ans = Math.max(p1, p2);
dp[i][z][o] = ans;
return ans;
}
var findMaxForm = function(strs, m, n) {
let len = strs.length;
let dp = Array.from({length: len + 1}, () => Array.from({length: m + 1}, () => Array.from({length: n + 1}, () => 0)));
for (let i = len - 1; i >= 0; i--) {
zerosAndOnes(strs[i]);
for (let z = 0, p1, p2; z <= m; z++) {
for (let o = 0; o <= n; o++) {
p1 = dp[i + 1][z][o];
p2 = 0;
if (zeros <= z && ones <= o) {
p2 = 1 + dp[i + 1][z - zeros][o - ones];
}
dp[i][z][o] = Math.max(p1, p2);
}
}
}
return dp[0][m][n];
};
var findMaxForm = function(strs, m, n) {
let len = strs.length;
let dp = Array.from({length: m + 1}, () => Array.from({length: n + 1}, () => 0));
strs.forEach(s => {
zerosAndOnes(s);
for (let z = m; z >= zeros; z--) {
for (let o = n; o >= ones; o--) {
dp[z][o] = Math.max(dp[z][o], 1 + dp[z - zeros][o - ones]);
}
}
})
return dp[m][n];
};盈利计划(多维费用背包)
js
package class069;
// 盈利计划(多维费用背包)
// 集团里有 n 名员工，他们可以完成各种各样的工作创造利润
// 第 i 种工作会产生 profit[i] 的利润，它要求 group[i] 名成员共同参与
// 如果成员参与了其中一项工作，就不能参与另一项工作
// 工作的任何至少产生 minProfit 利润的子集称为 盈利计划
// 并且工作的成员总数最多为 n
// 有多少种计划可以选择？因为答案很大，答案对 1000000007 取模
// 测试链接 : https://leetcode.cn/problems/profitable-schemes/
public class Code02_ProfitableSchemes {
// n : 员工的额度，不能超
// p : 利润的额度，不能少
// group[i] : i号项目需要几个人
// profit[i] : i号项目产生的利润
// 返回能做到员工不能超过n，利润不能少于p的计划有多少个
public static int profitableSchemes1(int n, int minProfit, int[] group, int[] profit) {
return f1(group, profit, 0, n, minProfit);
}
// i : 来到i号工作
// r : 员工额度还有r人，如果r<=0说明已经没法再选择工作了
// s : 利润还有s才能达标，如果s<=0说明之前的选择已经让利润达标了
// 返回 : i.... r、s，有多少种方案
public static int f1(int[] g, int[] p, int i, int r, int s) {
if (r <= 0) {
// 人已经耗尽了，之前可能选了一些工作
return s <= 0 ? 1 : 0;
}
// r > 0
if (i == g.length) {
// 工作耗尽了，之前可能选了一些工作
return s <= 0 ? 1 : 0;
}
// 不要当前工作
int p1 = f1(g, p, i + 1, r, s);
// 要做当前工作
int p2 = 0;
if (g[i] <= r) {
p2 = f1(g, p, i + 1, r - g[i], s - p[i]);
}
return p1 + p2;
}
public static int mod = 1000000007;
public static int profitableSchemes2(int n, int minProfit, int[] group, int[] profit) {
int m = group.length;
int[][][] dp = new int[m][n + 1][minProfit + 1];
for (int a = 0; a < m; a++) {
for (int b = 0; b <= n; b++) {
for (int c = 0; c <= minProfit; c++) {
dp[a][b][c] = -1;
}
}
}
return f2(group, profit, 0, n, minProfit, dp);
}
public static int f2(int[] g, int[] p, int i, int r, int s, int[][][] dp) {
if (r <= 0) {
return s == 0 ? 1 : 0;
}
if (i == g.length) {
return s == 0 ? 1 : 0;
}
if (dp[i][r][s] != -1) {
return dp[i][r][s];
}
int p1 = f2(g, p, i + 1, r, s, dp);
int p2 = 0;
if (g[i] <= r) {
p2 = f2(g, p, i + 1, r - g[i], Math.max(0, s - p[i]), dp);
}
int ans = (p1 + p2) % mod;
dp[i][r][s] = ans;
return ans;
}
public static int profitableSchemes3(int n, int minProfit, int[] group, int[] profit) {
// i = 没有工作的时候，i == g.length
int[][] dp = new int[n + 1][minProfit + 1];
for (int r = 0; r <= n; r++) {
dp[r][0] = 1;
}
int m = group.length;
for (int i = m - 1; i >= 0; i--) {
for (int r = n; r >= 0; r--) {
for (int s = minProfit; s >= 0; s--) {
int p1 = dp[r][s];
int p2 = group[i] <= r ? dp[r - group[i]][Math.max(0, s - profit[i])] : 0;
dp[r][s] = (p1 + p2) % mod;
}
}
}
return dp[n][minProfit];
}
}子数组最大累加和问题与扩展
java
package class070;
// 子数组最大累加和
// 给你一个整数数组 nums
// 返回非空子数组的最大累加和
// 测试链接 : https://leetcode.cn/problems/maximum-subarray/
public class Code01_MaximumSubarray {
// 动态规划
public static int maxSubArray1(int[] nums) {
int n = nums.length;
// dp[i] : 子数组必须以i位置的数做结尾，往左能延伸出来的最大累加和
int[] dp = new int[n];
dp[0] = nums[0];
int ans = nums[0];
for (int i = 1; i < n; i++) {
dp[i] = Math.max(nums[i], dp[i - 1] + nums[i]);
ans = Math.max(ans, dp[i]);
}
return ans;
}
// 空间压缩
public static int maxSubArray2(int[] nums) {
int n = nums.length;
int ans = nums[0];
for (int i = 1, pre = nums[0]; i < n; i++) {
pre = Math.max(nums[i], pre + nums[i]);
ans = Math.max(ans, pre);
}
return ans;
}
}子数组中找到拥有最大累加和的子数组
java
// 如下代码为附加问题的实现
// 子数组中找到拥有最大累加和的子数组
// 并返回如下三个信息:
// 1) 最大累加和子数组的开头left
// 2) 最大累加和子数组的结尾right
// 3) 最大累加和子数组的累加和sum
// 如果不止一个子数组拥有最大累加和，那么找到哪一个都可以
public static int left;
public static int right;
public static int sum;
// 找到拥有最大累加和的子数组
// 更新好全局变量left、right、sum
// 上游调用函数可以直接使用这三个变量
// 相当于返回了三个值
public static void extra(int[] nums) {
sum = Integer.MIN_VALUE;
for (int l = 0, r = 0, pre = Integer.MIN_VALUE; r < nums.length; r++) {
if (pre >= 0) {
// 吸收前面的累加和有利可图
// 那就不换开头
pre += nums[r];
} else {
// 吸收前面的累加和已经无利可图
// 那就换开头
pre = nums[r];
l = r;
}
if (pre > sum) {
sum = pre;
left = l;
right = r;
}
}
}打家劫舍
java
package class070;
// 数组中不能选相邻元素的最大累加和
// 给定一个数组，可以随意选择数字
// 但是不能选择相邻的数字，返回能得到的最大累加和
// 测试链接 : https://leetcode.cn/problems/house-robber/
public class Code02_HouseRobber {
// 动态规划
public static int rob1(int[] nums) {
int n = nums.length;
if (n == 1) {
return nums[0];
}
if (n == 2) {
return Math.max(nums[0], nums[1]);
}
// dp[i] : nums[0...i]范围上可以随意选择数字，但是不能选相邻数，能得到的最大累加和
int[] dp = new int[n];
dp[0] = nums[0];
dp[1] = Math.max(nums[0], nums[1]);
for (int i = 2; i < n; i++) {
dp[i] = Math.max(dp[i - 1], Math.max(nums[i], dp[i - 2] + nums[i]));
}
return dp[n - 1];
}
// 空间压缩
public static int rob2(int[] nums) {
int n = nums.length;
if (n == 1) {
return nums[0];
}
if (n == 2) {
return Math.max(nums[0], nums[1]);
}
int prepre = nums[0];
int pre = Math.max(nums[0], nums[1]);
for (int i = 2, cur; i < n; i++) {
cur = Math.max(pre, Math.max(nums[i], prepre + nums[i]));
prepre = pre;
pre = cur;
}
return pre;
}
}